$$2\cot4x = \cot2x \tan2x$$ Thank you in advance Thank you for the comments and hints I got an answer after many tries ;) Below is my answer Thank you $2cot4x = cot2x tan2x$ $2\frac{1}{tan 4x} = cot2x tan2x$ $2\frac{1}{\frac{2 tan 2x}{1 tan^2 2x}} = cot2x tan2x$ $2\frac{1 tan^2 2x}{2 tan 2x} = cot2x tan2x$So sec^2 (x)=1tan^2 (x) This is one of the three Pythagorean identities in trigonometry, but if you don't recognize it, try converting to sines and cosines 1/cos^2 (x)=1sin^2 (x)/cos^2 (x) Now, multiply each term by cos^2 (x) to get 1=cos^2 (x) sin^2Found 2 solutions by ewatrrr, MathLover1 Answer by ewatrrr () ( Show Source ) You can put this solution on YOUR website!

Answered 8 In Parts A To E Simplify The Bartleby
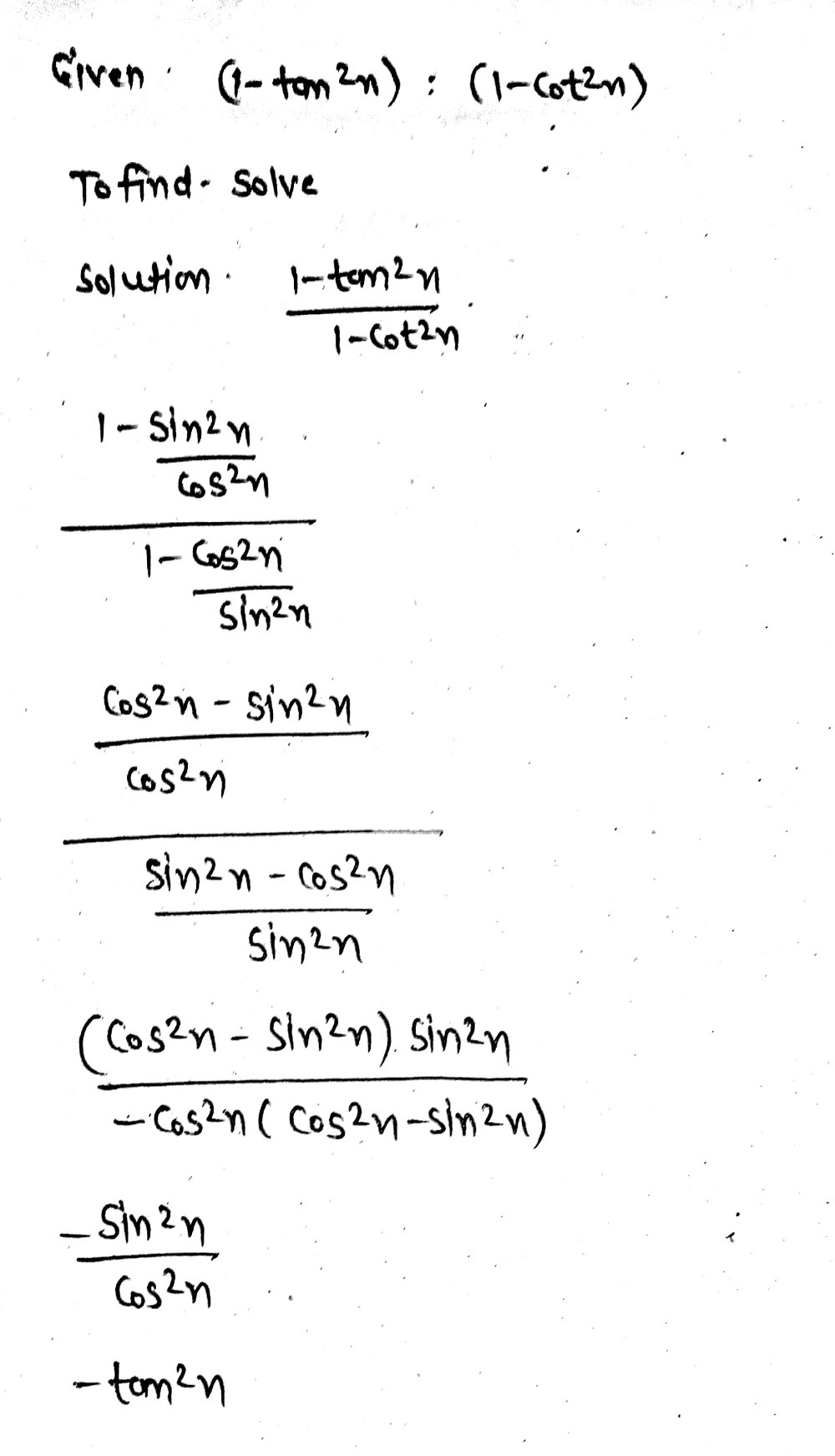
1-tan^2x/1-cot^2x=1-sec^2x
1-tan^2x/1-cot^2x=1-sec^2x-About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators Calculus 2, integral of (1 tan^2x) sec^2x, integral of cos(2x) Hi simplifying the following (sec^2x csc^2x) (tan^2x cot^2x) tan^2x = sec^2x 1 cot^2x = csc^2x 1 (sec^2x csc^2x) (sec^2x 1 csc^2x 1)= 2click here👆to get an answer to your question ️ if sec x sec^ 2x = 1 then the value of tan^ 8 tan^ 4 2tan^ 2x 1 will be equal tox = 1287 2 = the period of the function is the




How Many Can You Derive From First Principles Ppt Download
$\begingroup$ Well, if your instructor insisted that you do this by calling in the doubleangle formula, then I would replace my second paragraph with a criticism of the instructor for making things unnecessarily difficult Indeed, if the question had been to solve $\tan(9x/2)=1$, it would have been frustratingly difficult to use the ninefold angle formula and the halfangle formulas,Trigo Identities We should know that 1 (tan^2x)=sec^2x also 1 (cot^2x)=csc^2x Substituting these identities to the eqn (tan^2x) (cot^2x)= (sec 1 tan2x= 1sin2x/cos2x Find common denominator which is cos2x cos2x/cos2x sin2x/cos2x (cos2x sin2x)/cos2x 1cot2x = 1 cos2x/sin2x Common denominator is sin2x sin2x/sin2x cos2x/sin2x ( sin2x cos2x)/sin2x 1/(cosx2 sin2x)/cos2x 1/( sin2x cos2x)/sin2x
See the answer See the answer See the answer done loading Show transcribed image text Expert Answer Who are the experts?Giải phương trình 1, \(2\tan^2x3\tan x 2\cot^2x3\cot x 2=0\) 2, \(\cos^23x\cos2x\cos^2x=0\) 3, \(\cos^22x2\left(\cos x \sin x\right)^23\sin2x 1=0\) 4, \(1Sin(a/2)= square root of (1cos(a))/2 Since the radical is on the right side of the equation , switch the sides so it is on the left side of the equation To remove the radical on the left side of the equation , square both sides of the equation
Mylove mylove Mathematics High School answered Cot^2xtan^2x=1 for all values of x true or false?Hi Simplifying the following (sec^2x csc^2x) (tan^2x cot^2x) tan^2x = sec^2x 1 cot^2x = csc^2x 1 (sec^2x csc^2x) (sec^2x 1 csc^2x 1)= 2Chứng minh đẳng thức (tan^3x/sin^2x)(1/sinxcosx) (cot^3x/cos^2x)=tan^3x cot^3x




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 11 Trigonometric Equations Download Free Pdf




Tan 3x 1 Tan 2x Cot 3x 1 Cot 2x Secx Cosecx 2sincosx Brainly In
A=√sin2x(1 cotx) cos2x(1 tanx) B=sin^2xtan^2x/cos^2xcot^2x CẦN GẤP ẠAnswers Click here to see ALL problems on Trigonometrybasics Question tan^2xcot^2x=sec^2xcsc^2x Answer by jojo (1513) ( Show Source ) You can put this solution on YOUR website!Answers pineapplepizaaaaa Here for a good time of free question carrieaj08 no association stepbystep explanation




1 1 Csc Or Sin Or Csc Sin 1 Sin Csc X X X X X X 1 1 Sec Or Cos Or




Int Cos8x 1 Tan2x Cot2x Dx Youtube
Here, the problem is (cot^2 x 1)/ (tan^2 x 1) so cotx = 1/tanx by putting the value of cotx in above equation the simplified equation is (1 tan^2 x)/ (tan^2 x 1) (tan^2 x) (tan^2 x 1)/ (tan^2 x 1) (tan^2 x) 1/tan^2 x cot^2 x that should be the(tan x cot x)^2 = tan^2 x 2 tan x cot x = tan^2x cot^2x = (tan^2x 1) (cot^2 ) = This problem has been solved!Question prove the following identity cos2A = 2cos^2A 1 Answer by sarah_adam (1) ( Show Source ) You can put this solution on YOUR website!
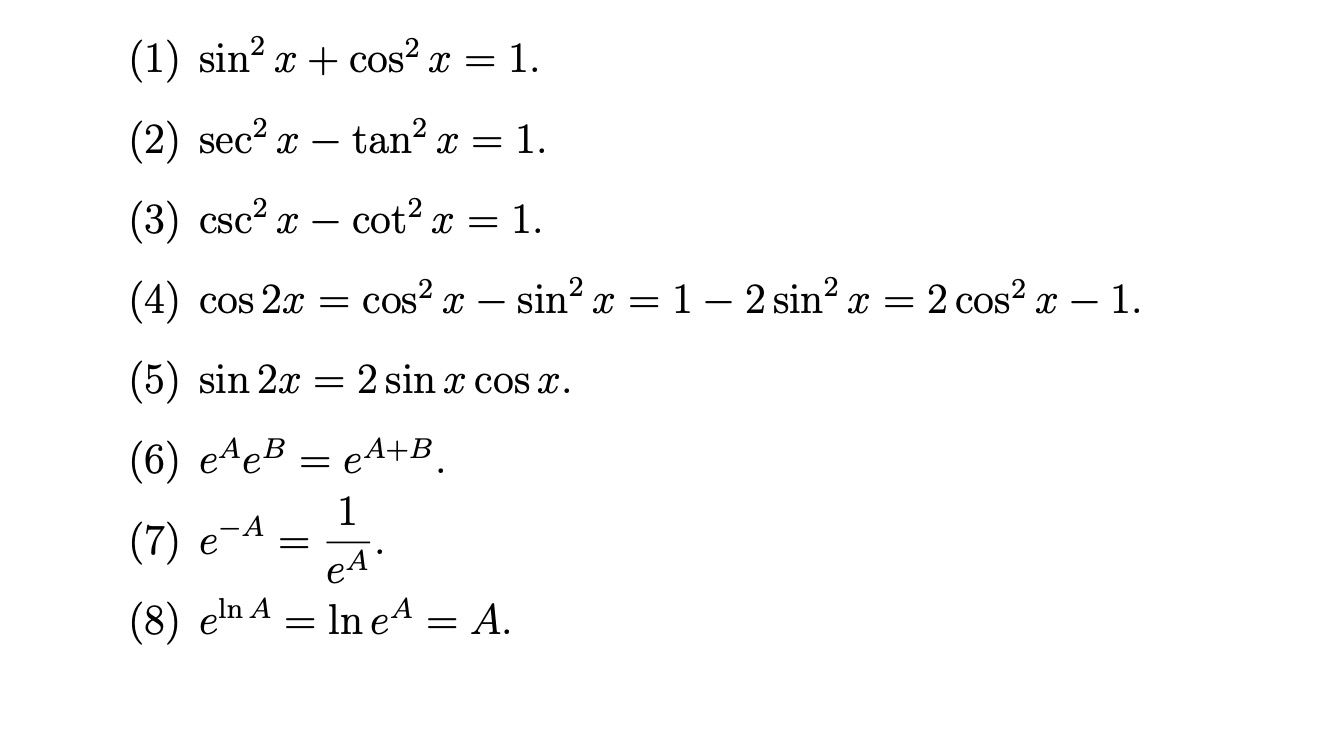



Here Is A List Of Identities Involving Trigonometric Chegg Com




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
Cos2A = Cos (AA) we know the formula for Cos (AB)=CosACosBSinASinB therefore Cos (AA)= CosACosA SinASinA = Cos^2A Sin^2A WE also know that Cos^2A Sin^2A = 1Prove each identity a) 1cos^2x=tan^2xcos^2x b) cos^2x 2sin^2x1 = sin^2x I also tried a question on my own tan^2x = (1 – cos^2x)/cos^2x RS= sin^2x/cos^2x I know that the Pythagorean for that is sin^2x cos^2x That's all I could do Trigonometry Express sec2x in terms of tanx and secx I know you have to sec(2x) = 1/cos(2x) = 1/(cos²x sin²x) But how do you split that Like how to simplify that?



Www Assignmentexpert Com Homework Answers Mathematics Answer Pdf




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified
Find an answer to your question Cot^2xtan^2x=1 for all values of x true or false?Cot^2xcsc^2x=1 for all values of x true or falsse Question Cot^2xcsc^2x=1 for all values of x true or falsseExperts are tested by Chegg as specialists in their subject area We review their content and use




Assignment 5 Fall 18 Studocu




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube
Chứng minh biểu thức sau độc lập với x \(\frac{\tan ^2x\cos ^2x}{\sin ^2x}\frac{\cot ^2x\sin ^2x}{\cos ^2x}\)Answered 2 years ago Author has 367 answers and 1508K answer views Start by simplifying cot^2 x 1 = cos^2 x/sin^2 x 1 = (cos^2x sin^2x)/sin^2 x = cos2x/sin^2x Next step, simplify tan2x * cot^2 xtan2x = tan2x (cot^2x1)=tan2x*cos2x/sin^2 x = sin 2x/sin^2 x1) sin3x = 0 2) cos 2 5x = 0 3) tan (x 15 o) = 3tan (x 15 o) 4) cos x cos 2x cos 3x = 0 5) sin 2x sin 4x sin 6x = 0 6) tan x tan 2x tan xtan 2x = 1 7) tan x tan 2x tan 3x = tan xtan 2xtan 3x 8) cot 2 x 3 sin x 3 sin x 3 = 0 Lớp 11 Toán



1




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco
Answer (2) 2 Solution (cot x – tan x)/ cot 2x = tan 2x (1/tan x) – tan x = tan 2x (1 – tan 2 x)/tan x = tan 2x (1 – tan 2 x)/ 2 tan x 2 Using the formula tan 2A = 2 tan A/ (1 – tan 2 A) = 2 tan 2x (1/tan 2x) = 2Cosx(tan^2x1)=secx Answer by jim_thompson5910() (Show Source) You can put this solution on YOUR website! Cot^2xtan^2x=1 for all values of x true or false?




Trigonometry Reciprocal Identities Expii




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples
Trigonometric Simplification Calculator \square!Verify the Identity cot (x)^2 (sec (x)^21)=1 cot2 (x) (sec2 (x) − 1) = 1 cot 2 ( x) ( sec 2 ( x) 1) = 1 Start on the left side cot2(x)(sec2(x)−1) cot 2 ( x) ( sec 2 ( x) 1) Apply pythagorean identity cot2(x)tan2(x) cot 2 ( x) tan 2 ( x) Convert to sines and cosines Tap for more steps Write cot ( x) cot ( x) in sines and cosinesFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor



Web Auburn Edu Holmerr 1617 Textbook Lhopital Print Pdf




If Tan X Cot X 2 Find The Value Of Tan2 X Cot2 X Brainly In
This is what I've got so far sin = 1/csc tan = 1/cot 1cot2(x) = csc2(x) 1/1cot2(x) = 1/csc2(x) trig For each expression in column I, choose the expression from column II to complete an identity Column I Column II 1 tanxcosx A sin^2x/cos^2x 2 sec^2x1 B 1/sec^2x 3 sec x/cscx C sin(x) 4 1sin^2x Dcsc^2xcot^2xsin^2x 5 cos^2 x E Prove the following identities $$(\sec^2 x \tan^2x)(\csc^2 x \cot^2x) = 1 2 \sec^2x \csc^2 x \tag i$$ $$\frac{\cos x}{1\tan x} \frac{\sin x}{1\cot x} = \sinMath please help quick Which of the following are identities?




Derive 1 Tan 2x Sec 2x And 1 Cot 2x Text Cosec 2x Geometrically Mathematics Stack Exchange



Http Www Pitt Edu Evt3 Triviums Trigonometry Trivium Pdf
1 cos ( x) − cos ( x) 1 sin ( x) = tan ( x) Go!Tan2x Formula Trigonometric Formulas like Sin 2x, Cos 2x, Tan 2x are known as double angle formulas because these formulas have double angles in their trigonometric functions Let's discuss Tan2x Formula Tan2x Formula = 2 tan x 1 − t a n 2 xFree math lessons and math homework help from basic math to algebra, geometry andFind all solutions of sec^2xtan^2x=3 in the interval 0,2pi Since tan^2 = sec^2 1 you get sec^2 sec^21 = 3 2sec^2= 4 sec^2 = 2Check all that apply (Points 2) sin2x = 1 cos2x sin2x cos2x = 1 tan2x = 1 sec2x cot2x = csc2x 1 Question 4 4




Answered 52 Csc X Cscx Dx Tan 2x Tan 2x Bartleby



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf
Cot^2x tan^2x = 1 for all values of x False Cos2A = 2cos^2A1 for all values of x True Sin(x)=cosx for all values of x False Cos(AB)=cosAcosBsinAsinB True Trigonometric equations and trigonometric identities are the same thing False _____cos B = 1/2 cos(AB)cos (AB) cos AProve each identity a) 1cos^2x=tan^2xcos^2x b) cos^2x 2sin^2x1 = sin^2x I also tried a question on my own tan^2x = (1 – cos^2x)/cos^2x RS= sin^2x/cos^2x I know that the Pythagorean for that is sin^2x cos^2x That's all I could do trig tan^2 x1=sec^2x So to get 1 on the other side of the equal sign wouldn't it be sec^2xtan^2x=1?




Lim X Rightarrow Frac Pi 2 Frac Tan 2x Scholr




Prove That Tan 2 2x Tan 2 X1 Tan 2 2x Tan 2 X Tan 3x Tan X
Answer by stanbon (757) ( Show Source ) You can put this solution on YOUR website! Find an answer to your question If 2tanx/ (1tan^2x) = 1, then x can equal ____ Check all that apply A) x=5pi/8 npi B) x=pi/8 npi C) x=3pi/8 npi D) x=7p tan^2x (1tan^2x)/(1cot^2x) 1) First, notice that both the numerator and denominator are Pythagorean Identities Proceed to change them sec^2x/csc^2x 2) Turn into sine and cosine Then multiply




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
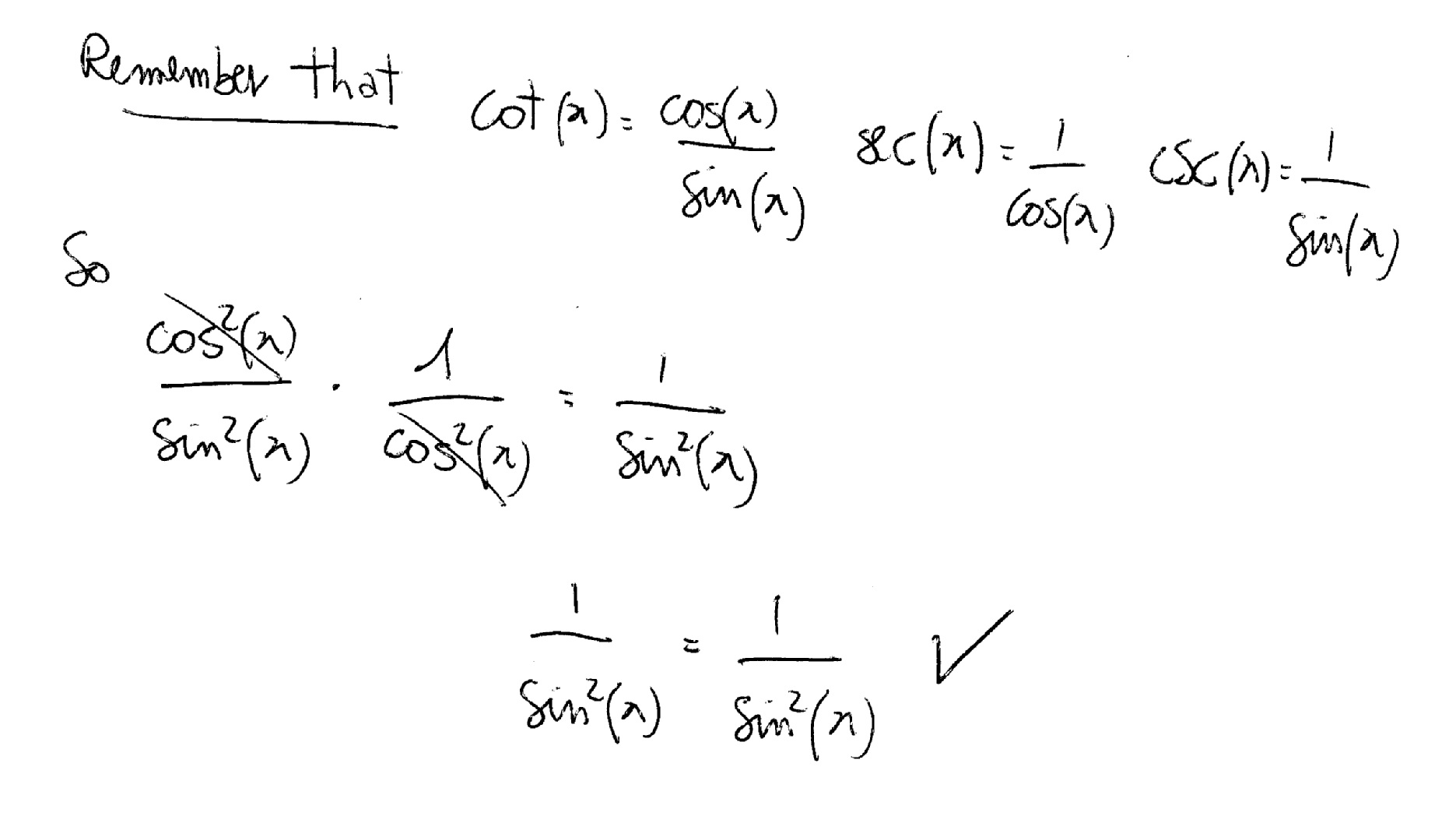



How Do You Verify Cot 2x Sec 2x Csc 2x Socratic
This question was just answered and I'm not sure if this is the same person or not If so, please let me know where you're stuck andSimplify (tan (2x))/ (1cot (2x)) tan (2x) 1 − cot(2x) tan ( 2 x) 1 cot ( 2 x) Nothing further can be done with this topic Please check the expression entered or try another topicGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




How Many Can You Derive From First Principles Ppt Download




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic
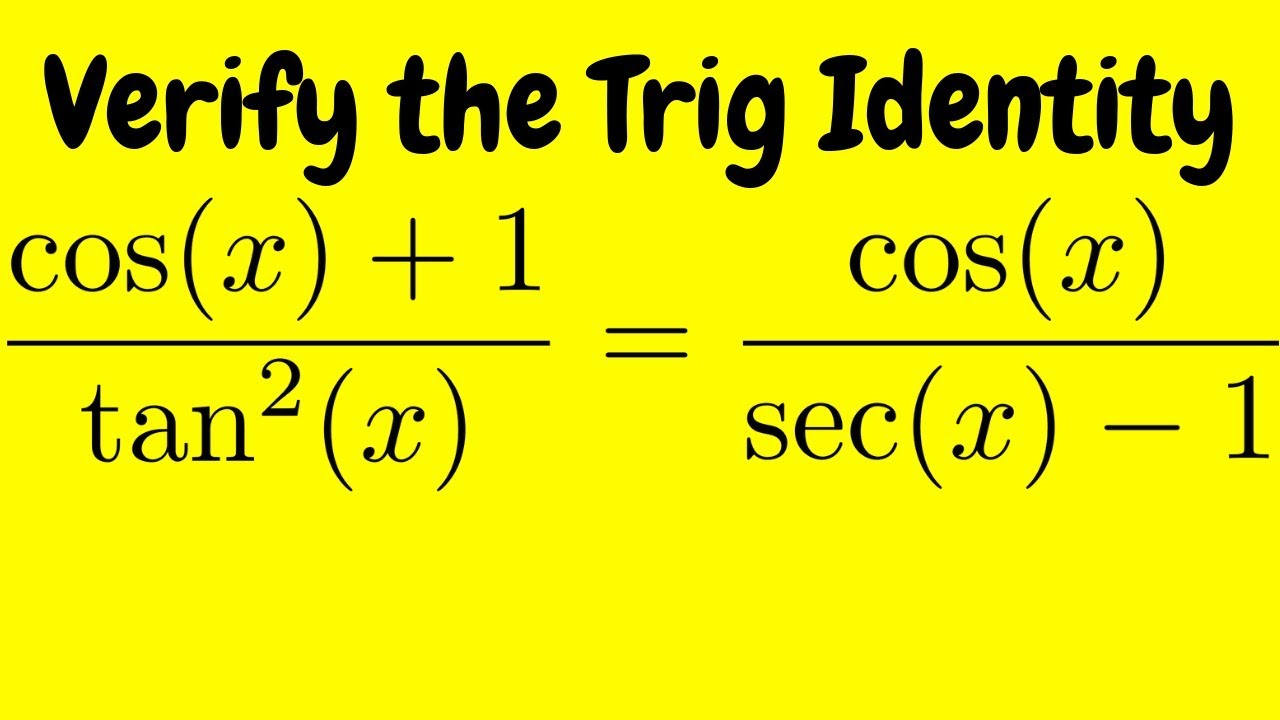



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube




Trigonometry Questions For All Competitive Examinations




Solve Tan 2x Cot 2x Sec 2x Sin 2x Cos 2x Cosec 2x Is Brainly In



1



2




Derivative Of Tan X Old Video Khan Academy



Tan 2x Tan 2x
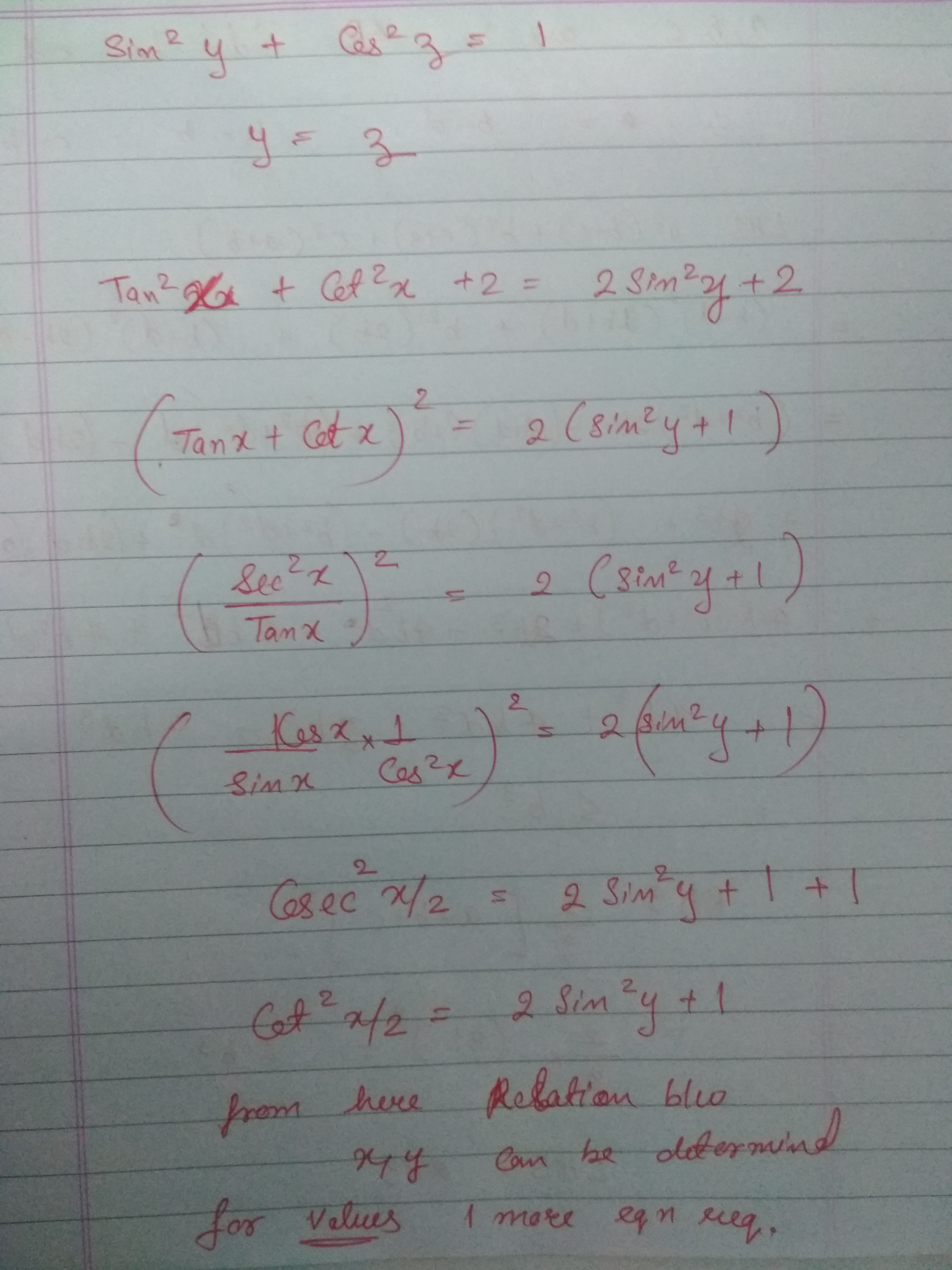



Solve For X Y And Z If Tan 2x Cot 2x 2sin 2y And Sin 2y Cos 2z 1 Askiitians
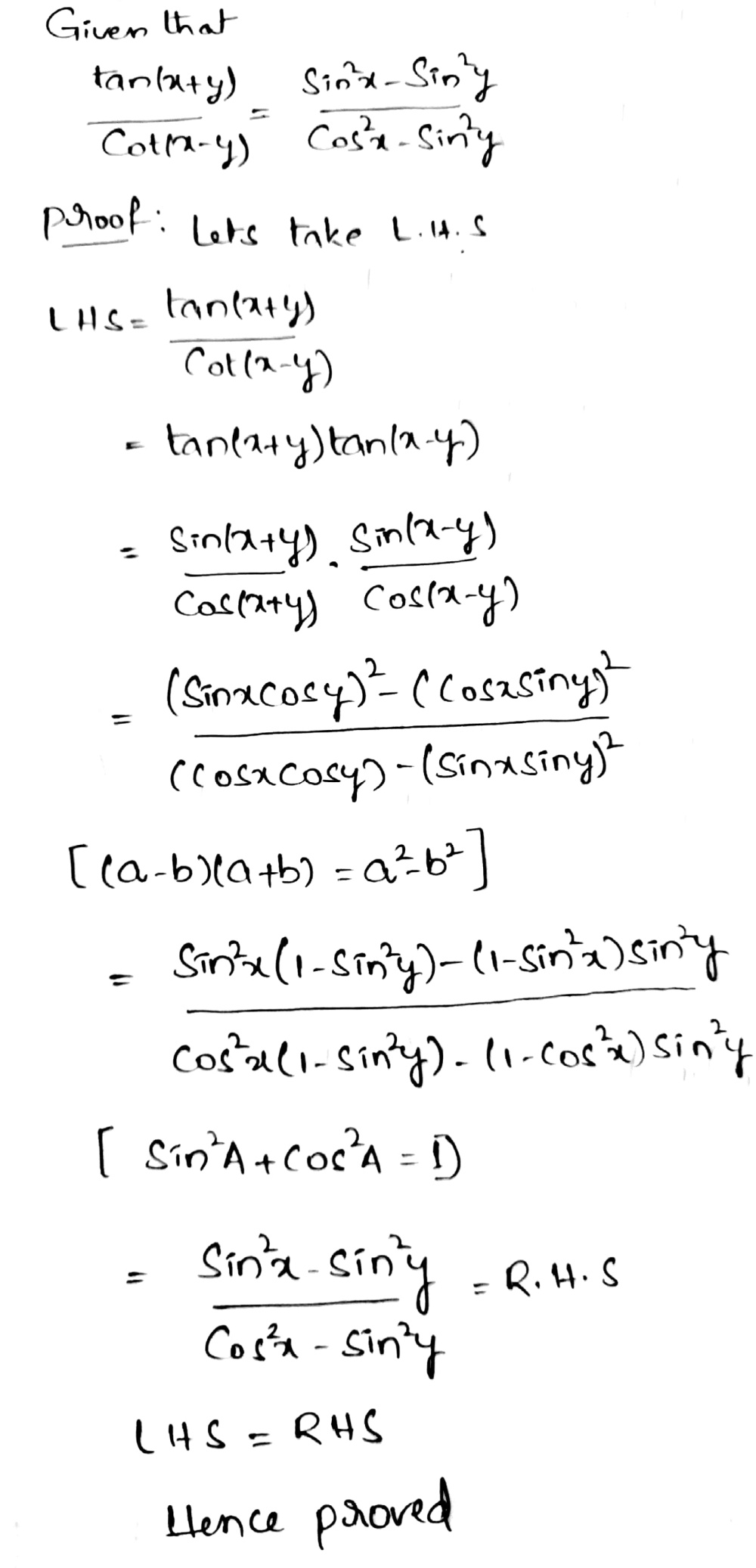



Prove Each Of The Following Frac Tan X Y Cot X Y Frac Sin 2x Sin 2y Cos 2x Sin 2y Frac Tan 2x Tan 2y 1 Tan 2xtan 2y Snapsolve




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



2




1 Sin 2x Tan 2x Sec Sec 2 X Csc 2x 1 1 C Gauthmath




The Expression Tan 4x Tan 2x 1 Tan 4x Tan 2x Chegg Com



Http Www Math Brown Edu Tomg Formulas Pdf



Http Www Stevejonak Com Test03 Addtional Review Pdf
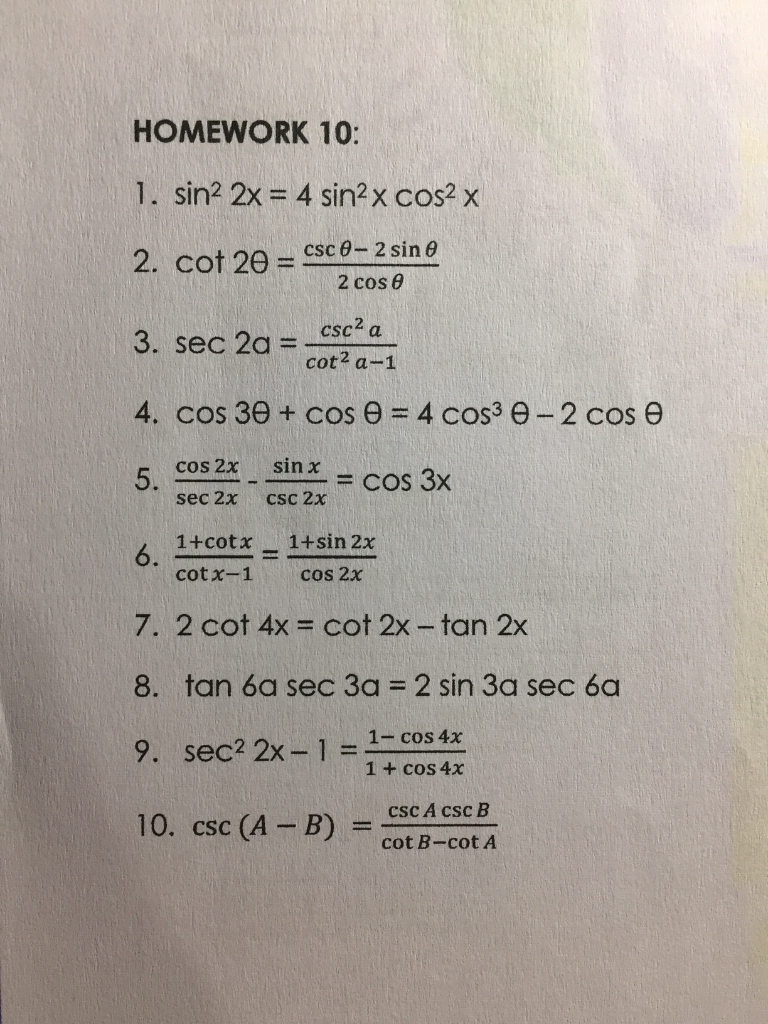



Homework 10 1 Sin2 2x 4 Sin2 X Cos2 X Csc 2 Sin Chegg Com



2




In The Integral Int Cos 8x 1 Cot 2x Tan 2x Dx A Cos 8x K Where K Is An Arbitrary Constant Youtube




Tan 3x 1 Tan 2x Cot 3x 1 Cot 2xhope It Helps U Welltq Brainly In




Ppt Analytic Trig Powerpoint Presentation Free Download Id
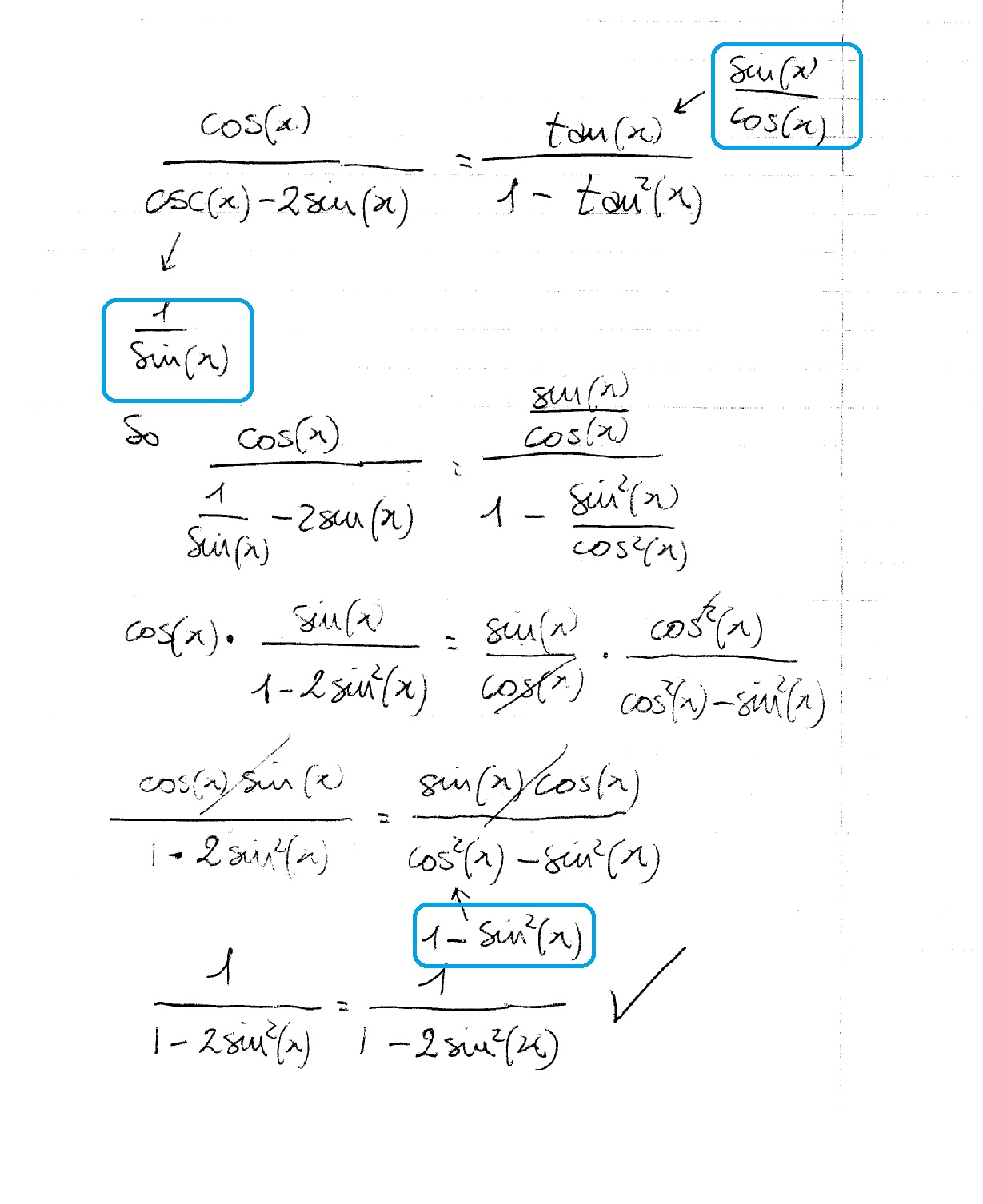



How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic




Trigonometry 1



Knoxschools Instructure Com Files 7731 Download Download Frd 1 Verifier Nwvnfhcqjj3uwbxvthab5cvl9gai66hcxz8iywsc
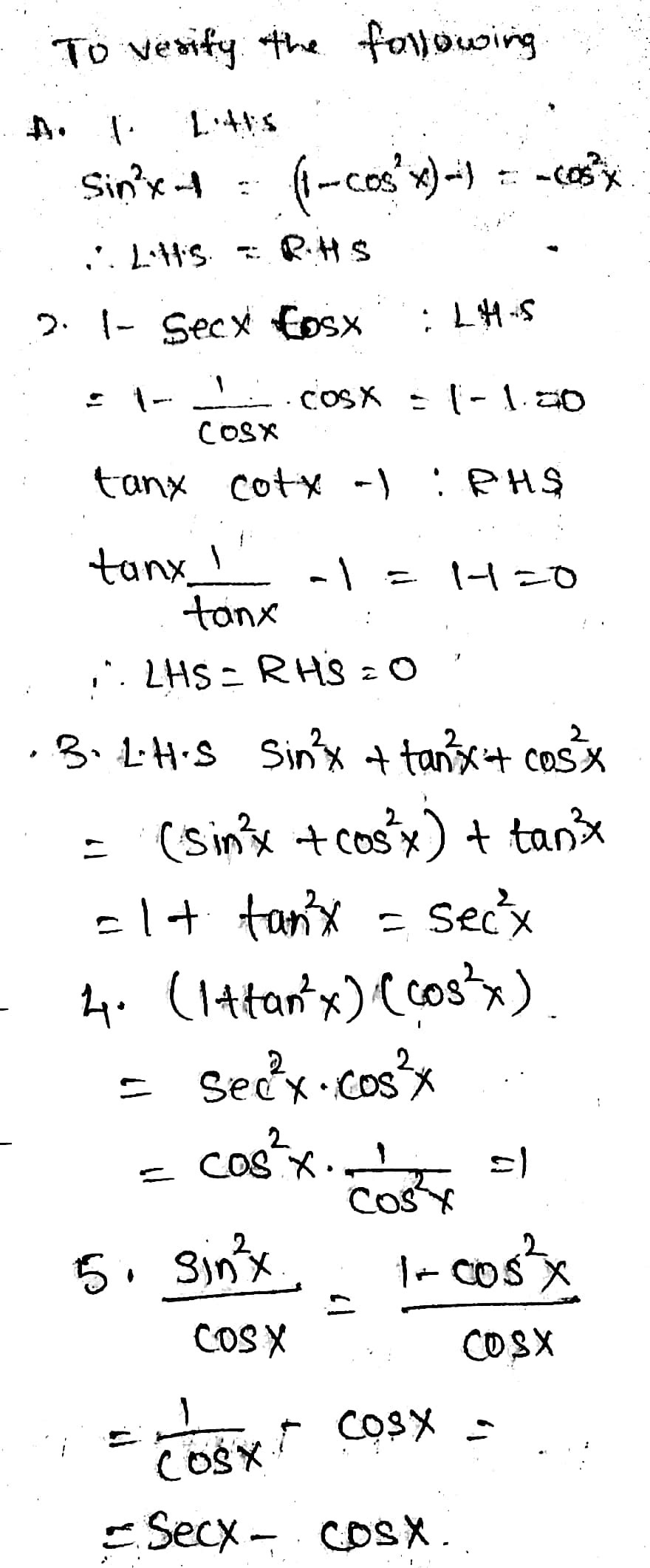



Directions Verify The Following Trigonometric Id Gauthmath



3




Int 1 Tan 2 X 1 Cot 2 X Dx




Misc 44 Value Fo Tan 1 2x 1 1 X X2 Dx Is Miscellaneous




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples




Integration Trig Identities Ppt Download




Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples



Http Www Mpsaz Org Mtnview Staff Clpavlovic Collegealgebra Resources Files Assignment 6 3 Day 1 3 Worksheet Key Pdf




Answered 8 In Parts A To E Simplify The Bartleby



1 If Fx Sin 2x Cos 2x Sec 2x Csc 2x Tan 2x Cot 2x Gauthmath



2



2



How To Prove The Identity In Tanx Cotx 2 Sin2x Quora



Http Theprofessorshut Weebly Com Uploads 2 3 2 7 Pc Chap 6 Sect 2 Sum Difference And Cofunction Identities Pdf




If Cos 2x Cos 4x 1 Then The Value Of Tan 4x Cot 4x Tan 2x Cot 2x Is Equal To Detailed Brainly In




Tan 2x Cot 2x 2
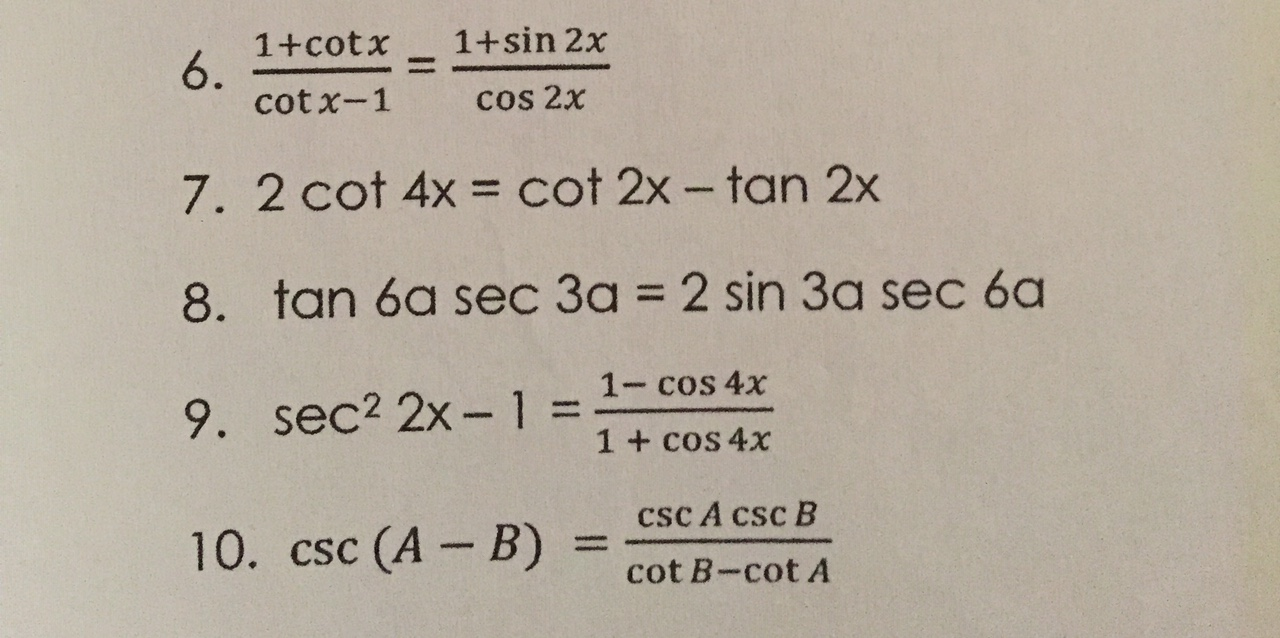



1 Cotx 1 Sin 2x 6 Cotx 1 Cos 2x 7 2 Cot 4x Cot 2x Chegg Com




Trig Identities Ppt Download




Verify The Given Identity Tan 2x 2 Cot X Tan X Chegg Com



Solved K U 1 Differentiate The Following Choose 4 Only Marks A Y Tan 2x 1 Cot 2x B F X Xsin X 1 X C G X Sec Quot 6x Cos Course Hero




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic



Http Www Berkeleycitycollege Edu Wp Wjeh Files 12 01 Tri Exercise Identity Pdf



Search Q Trig Identities Tbm Isch




Prove That Sec 2x Cosec 2x Tan 2x Cot 2x



Www Cbsd Org Cms Lib Pa Centricity Domain 40 Final review 3 hpc notes Pdf




Cot X Cos 2 X Tan X Sin 2 X 2 Cot 2x Youtube




Prove The Identity 1 Tan 2x 1 Tan 2x 1 2sin 2x In Urdu Hindi Youtube




Dana Harrington Benjamin Leis Thanks So Much For Responding But I Don T Think That S The Case All 6 Solutions Work In The Original Equation When Subbed In Also When You Graph




Tinkutara Equation Editor Math Forum Question




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




5 Tan X Tan 2x Dx Select One A 1 2 H Tan 2 X Chegg Com




Prove The Following Identities Tan 3 X1 Tan 2 X Cot 3 X1 Cot 2 X 1 2sin 2 Xcos 2 Xsinxcosx
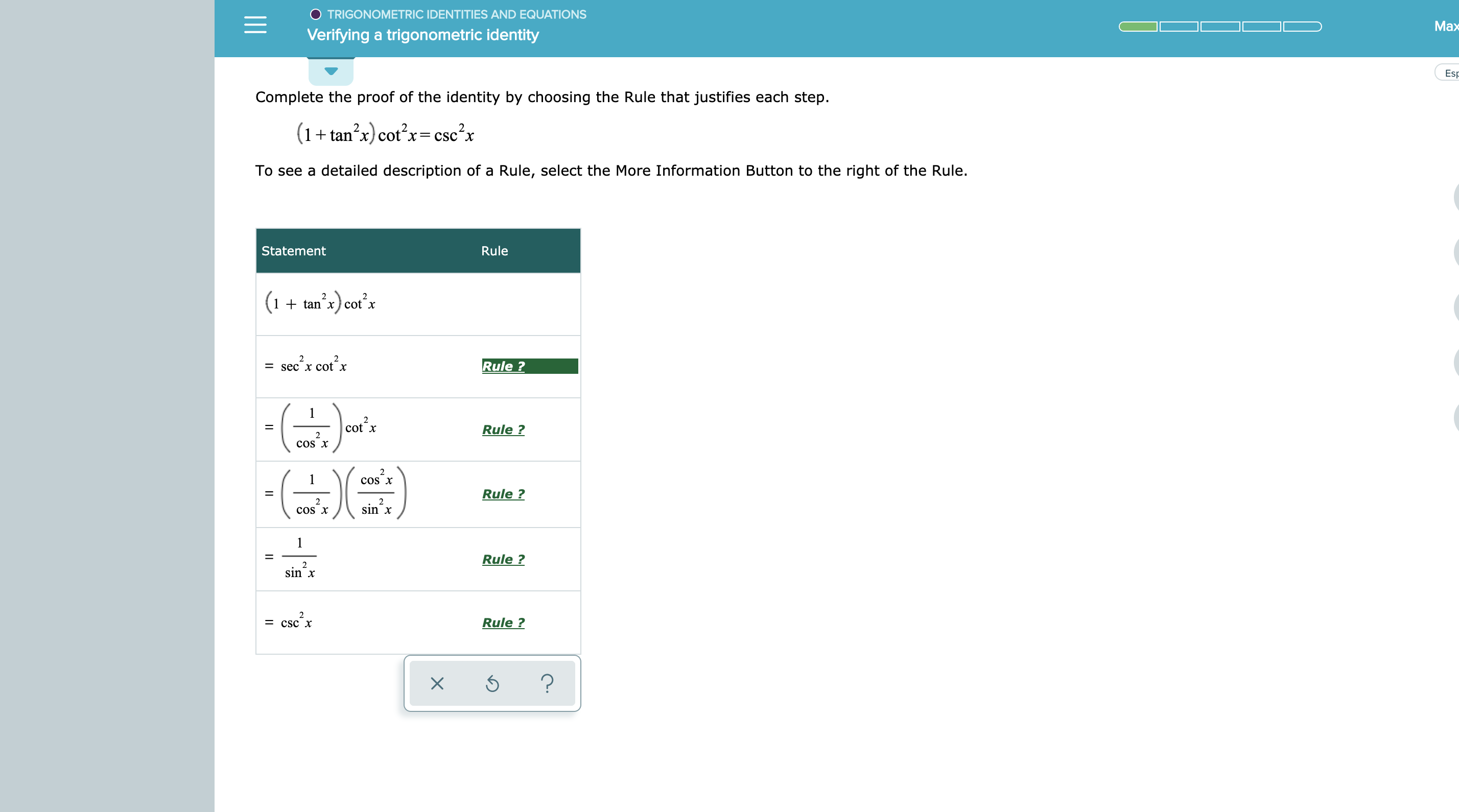



Answered Trigonometric Identities And Equations Bartleby




Chứng Minh Rằng Tan 2 X Cot 2 X Frac 6 2cos4x 1 Cos4x Cau Hỏi Hoidap247 Com




17 Tan 2x Cot 2x Sec 2x Cos Ec2x Gauthmath



Solved If Sin2x 3 5 Find All Possible Values Of Sin X Tan X Cos X Cot X Sec X Csc X If Cosx 3 5 Find All Possible Values Of Sin2x Tan2x Course Hero




The Derivative Of Sec2x Derivativeit




Consider The Following Equations 1 Cosec 2x Sec 2x Cosec 2xsec 2x 2 Sec 2x Tan 2x Sec 2xtan 2x 3 Cosec 2x Tan 2x Cot 2x
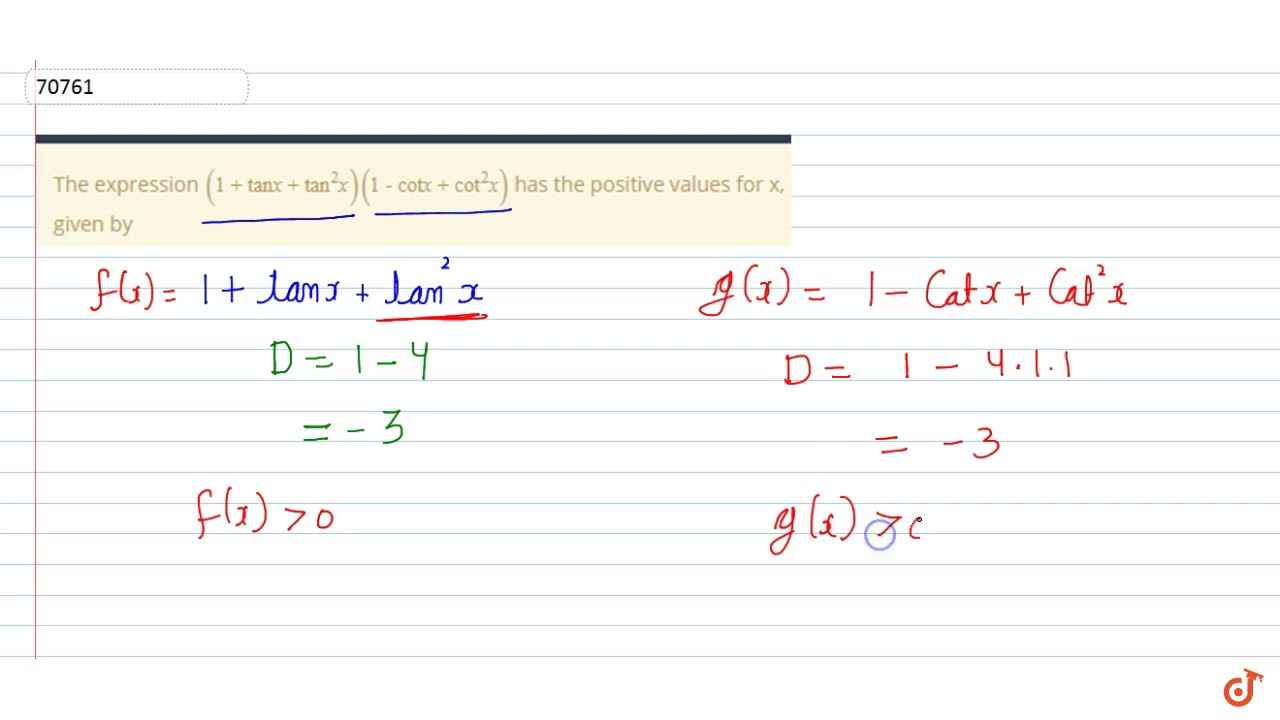



The Expression 1 Tan X Tan 2 X 1 Cot X Cot 2 X Has The Positive Values For X Given Youtube




Verify The Following Identities Sec2 Theta 1 Sec2 Chegg Com




Tan 2x Tan 2x
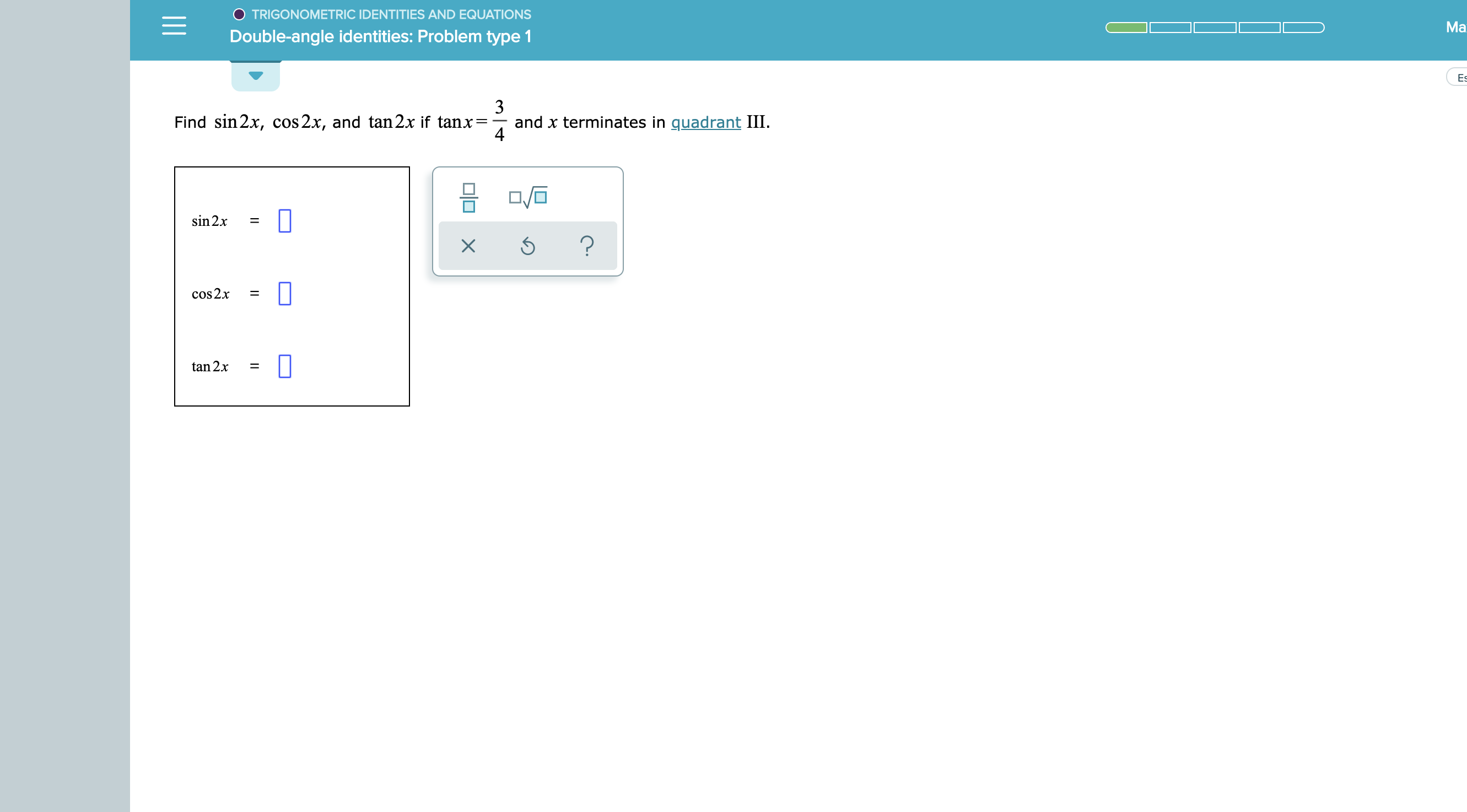



Answered O Trigonometric Identities And Bartleby



Cot2x To Tan2x The Student Room



Www Donovancatholic Org File Summer Math18 Review Incoming Calculus H Ap 18 Pdf




Tan 2x Cot 2x 2 Youtube




Integral Of Tan 2x Cot 2x 2 Calculus 1 Trig Integrals Calculus Mathematics Email Subject Lines



2



2




Cot X 2 Cot 2x Tan X Youtube




Int 1 Tan 2x 1 Cot 2x Dx
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf



1 Tan 2x 1 Cot 2x Gauthmath



Solved K U 1 Differentiate The Following Choose 4 Only Marks A Y Tan 2x 1 Cot 2x B F X Xsin X 1 X C G X Sec Quot 6x Cos Course Hero



0 件のコメント:
コメントを投稿